Synthetix Perps Dynamic Funding Rates

An essential aspect of the Synthetix Perps ecosystem is the dynamic funding rate, which aims to maintain delta neutrality in markets by integrating velocity and time into funding rate calculations. This novel approach brings a fresh perspective to risk management and funding rate computations. In this blog post, we will explore the inner workings of dynamic funding rates, explain the math behind the velocity, and provide a practical example.

Understanding Synthetix Perps

Synthetix Perps are decentralized perpetual futures contracts built utilizing Synthetix Liquidity, allowing traders to gain exposure to various assets without actually owning them. Perpetual futures, unlike traditional futures, have no expiry date, and traders can hold their positions indefinitely as long as they maintain sufficient margin. To guide markets toward balance, the Synthetix Perps system implements a dynamic funding rate mechanism and a price impact function. Before explaining the unique innovations behind dynamic funding rates, let's first understand the purpose of funding rates in perpetual futures.

Funding Rates

The role of funding rates in perpetual futures is generally to balance long and short demand. Traders will either pay or receive funding rates, depending on their positions. If the funding rate is positive, long position holders will pay the funding rate to those holding short positions, and vice versa.

The Dynamic Funding Rate

The dynamic funding rate, while sharing similarities with the traditional funding rate, has a few key differences. Instead of relying solely on market skew to determine the funding rate, the dynamic funding rate takes into account both velocity and market skew. This means that when there is a persistent long skew, funding rates will continue to increase over time. Conversely, when short positions dominate, funding rates will decrease as long as the short skew is maintained. By incorporating velocity into the funding rate calculation, this mechanism encourages traders to take positions opposite to the current market skew, promoting market stability and balance.

A Basic Example

The ETH Perp market currently has $100,000 in LONG positions and $20,000 in SHORT positions. Three scenarios can happen for this market from here:

- Skew stays long - No one enters (or exits) this market. Funding rates will continue drifting upwards. Longs pay shorts an increasing amount each hour.

- Skew becomes neutral - Traders bring the skew to neutral (100,000 LONG and 100,000 SHORT.) Funding rates will stay the same. Longs pay shorts the same amount each hour.

- Skew flips to short - Traders flip the skew to SHORT (50,000 LONG and 100,000 SHORT.) Funding rates will decrease. Longs pay shorts a decreasing amount each hour.

Calculating the Dynamic Funding Rate (Example)

In this example, we will calculate the dynamic funding rate for ETH using a hypothetical scenario with three trades. We will use the formula dr/dt = c * skew, which takes into account the new positions and the skew changes.

Here's the breakdown of the trades:

1. At Hour 0:

• User #1 longs 300 ETH
• User #2 shorts 150 ETH
• longOI = 300 ETH, shortOI = 150 ETH, skew = 150 ETH

2. At Hour 10:

• User #1 longs an additional 200 ETH
• longOI = 500 ETH, shortOI = 150 ETH, skew = 350 ETH

3. At Hour 15:

• User #2 shorts another 150 ETH
• longOI = 500 ETH, shortOI = 300 ETH, skew = 200 ETH

To calculate the funding rate velocity for each period, we use the formula dr/dt = c * skew, where dr/dt is the funding rate velocity, c is the constant factor (maxFundingVelocity / skewScale), and skew is the difference between long and short open interest (OI) positions.

1. From Hour 0 to Hour 10:

• User #1 longs 300 ETH, User #2 shorts 150 ETH
• longOI = 300 ETH, shortOI = 150 ETH, skew = 150 ETH long
• c = maxFundingVelocity / skewScale = 300% / 1000000 ETH
• fundingRateVelocity = c * skew = (300% / 10^6 ETH) * 150 ETH = 0.045% per day
• funding rate hour 0 - 0% (assuming it starts at 0%)
• funding rate hour 10 - (0.045% / 24) * 10 = 0.01875% (increasing linearly over 10 hours)

2. From Hour 10 to Hour 15:

• User #1 longs 200 ETH
• longOI = 500 ETH, shortOI = 150 ETH, skew = 350 ETH long (positive skew b/c long positions are higher)
• fundingRateVelocity = c * skew = (300% / 10^6 ETH) * 350 ETH = 0.105% per day
• funding rate hour 10 - .01875%
• funding rate hour 15 - 0.01875% + (0.105% / 24) * 5 = 0.028125% (increasing linearly over 5 hours)

3. From Hour 15 to Hour 20:

• User #2 shorts 150 ETH
• longOI = 500 ETH, shortOI = 300 ETH, skew = 200 ETH long (positive skew b/c long positions are higher)
• fundingRateVelocity = c * skew = (300% / 10^6 ETH) * 200 ETH = 0.060% per day
• funding rate hour 15 - 0.028125%
• funding rate hour 20 - 0.028125% + (0.060% / 24) * 5 = 0.033125% (increasing linearly over 5 hours)

4. From Hour 20 to Hour 24:

• User #3 shorts 500 ETH
• longOI = 500 ETH, shortOI = 800 ETH, skew = -300 ETH long (negative skew because short positions are higher)
• fundingRateVelocity (per day) = c * skew = (300% / 10^6 ETH) * -300 ETH = -0.090% per day
• funding rate hour 20 - 0.033125%
• funding rate hour 24 - 0.033125% + ((-0.090% / 24) * 4) = 0.030625% (decreasing linearly over 4 hours)

The Effects of Risk Management

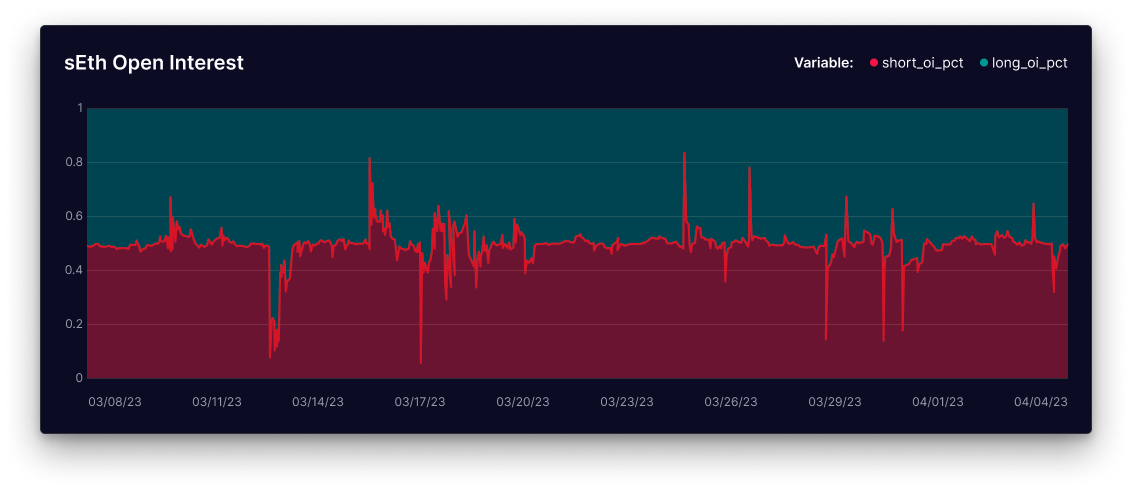
Effective risk management is essential in the Perps mechanism design. Liquidity providers must never be exposed to long-term skew; instead, they should utilize incentives such as Dynamic Funding Rates and Price Impact to properly encourage arbitrage traders to guide markets toward equilibrium.

The figure above illustrates the impact of these two features on Synthetix Perps' most popular market, sETH. The market maintains continuous neutrality, and liquidity providers (stakers) act as temporary counterparties. In summary, the design is functioning as intended.

Conclusion

Dynamic funding rates are vital to Synthetix Perps' risk management mechanism. By encouraging market neutrality, and protecting liquidity providers, it plays a critical role in maintaining the stability of Synthetix Perps.